slt 
est ce que? l equation différantielle de riccati devient equation de barnaulli si on l’ ecrit y`=a(x)y2+b(x)y et c(x)=0 stp aidez moi
اين انتم يا طلاب ريضيات السنة الثانية
- معادلة برنولي "Bernoulli ODE" .
طريقة الحل:
الفكرة تكمن بتحويلها اى معادلة تفاضلية خطية من المرتبة الأولى.. ويتم ذلك من خلال الأتي..
نقوم بالتحويلي الأتي :
فينتج لدينا 
وبالتعويض بالمعادلة السابقة ينتج لدينا المعادلة الخطية التالية:
ملاحظة: يجب أخذ يبعين الإعتبار إن كان
حلاً أما لا وفيما إذا كان خاص أم شاذ.مثال :
حل المعادلة التالية
بإستخدام الطريقة أعلاه لدينا
نفرض أنّ 
وبالتالي نحصل على المعادلة :
وهي معادلة تفاضلية خطية من المرتبة الأولى وحلها العام هو
وبالتالي يكون لدينا
والعلاقة الأخيرة هي الحل العام …..
ونلاحظ أنّ
هو حل للمعادلة …ولكنه حل شاذ لانه لا ينتج من الحل العام. - معادلة ريكاتي "Riccati ODE" .
طريقة الحل:
سنقوم بحل معادلة ريكاتي بتحويلها الى معادلة خطية من المرتبة الأولى.
وهذه الطريقة تعتمد على معرفة حل خاص لمعادلة ريكاتي.ليكن
حل خاص لمعادلة ريكاتي وبالتالي 
سنقوم الآن بإجراء التحويل التالي…
بالتعويض بالمعادلة أعلاه نجد أنّ:
نلاحظ أنّ المعادلة الأخيرة عبارة عن تفاضلية خطية من المرتبة الأولى.
ملاحظة: كان بالامكان تحويل معادلة ريكاتي الى معادلة برنولي من خلال الفرض
حيث انّ 
حل خاص لمعادلة ريكاتي. - اي استفسار راني هنا اوي اذا ما فهمتيش
ختي اشكرك كثيرا اسعدني اهتمامك جدا نحن لم نتطرق اولا في معادلة برنولي الى حالة اذا كان y=0ارجو ان تشرحيها لي ثانيا الملاحظة الاخيرة ماذا تعنيw في y=u+w شكرا مرة اخرى جزاك الله عني الف خير(ارجو ان تشرحي لي في اقرب وقت ممكن)
OK MA SEOUR
y=0في غالب الاحيان يكون حل لمعادلة برنولي
UNE équation de bernouli est une équation differentielle de la forme :
y’=a(x)*y+b(x)*y^a
ou:a et b sont des fonction de class c1 c-a-d dirivable et continue
a et un réel quelqhonq deffirent de 1 alors que a digne la puissance a-ieme de la fonction y
معادلة برنولي من الصورة 
. واضح ان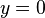 
هو حل للمعادلة.
نفرض ان 
، نقسم على 
:
نرمز 
أي 
، فنحصل على الدالة الخطية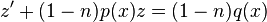 
.
نجد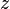 
ومنها يمككننا ايجاد 
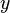– المتغير التابع المطلوب.
———————–
UNE équation de riccati est une équation differentielle de la forme :
ou: Où 
, 
et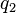 
sont trois fonctions de class c1 c-a-d dirivable et continue
Pour certaines conditions sur , , , 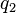l’équation est résoluble par quadrature. Grâce au théoréme de cauchy-liipschitz on prouve que, si , , 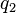sont des fonctions continues, alors il existe des solutions à l’équation de Riccati. Enfin on démontre que, si l’on en connaît une solution particulière, une équation de Riccati se ramène par changement de variable, à une equation de bernouli
معنى هذي الحكاية كامل
باستعمال نظرية كوشي و……الي معاه هههه نبرهنو بالي هادوك الدوال بالي ام مستميرين يسما او كاين حلول فالمعادة تاع ريكاتي ومن بعد نبينو ادا كا ن كاين حل خاص للمعادلة هادي معتنا معناتها المعادلة تاع برنولي نقدرو نخرجوها من معادلة تاع ريكاتي باستبدال المتغير
وهاذي لحكاية كامل :ملاحظة: كان بالامكان تحويل معادلة ريكاتي الى معادلة برنولي من خلال الفرض حيث انّ حل خاص لمعادلة ريكاتي.
w هادي اي دالة نفرضوها
ان شاء الله تكوني فهمتي
شكرا كثيرا اختي جزاك الله اللللللللللللللللللللللللف خير ان شاء الله يححق ربي ماتتمنا
|
المشاركة الأصلية كتبت بواسطة sara118
 شكرا كثيرا اختي جزاك الله اللللللللللللللللللللللللف خير ان شاء الله يححق ربي ماتتمنا
|
بلا مزية حنووووووووووووووووووووووووووووووووووووونة ما شي خسارة فيكم الي تحتاجي رانا هنا
امييييييييييييييييييييييييييييييييييييييييييين يا رب ربي يسمع منك يا رب
……………….
بارك الله فيكم